ANT

ANT (Atomistic NanoTransport) is a software package to compute the electrical current in atomically defined nanostructures. ANT combines self-consistent field electronic calculations (typically Density Functional Theory), Landauer transport and the (non-equilibrium) Greens functions formalisms.

At present, ANT software package is composed of the independent codes

• ANT.G
• ANT.1D
• ANT.U.

In ANT the target system is divided in three regions, see Figure 1:

• Left electrodes
• Device (scattering region)
• Right electrodes

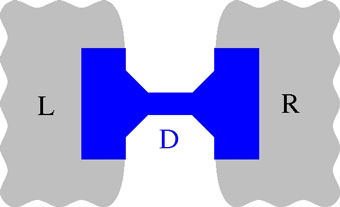
Figure 1. Schematic representation of system set up;  Left electrodes (L), device (D) and right electrodes (R).

ANT can compute the properties and phenomena needed for understanding the charge transport between bulk electrodes when these are connected by an atomic- or a molecular-size region and a bias voltage is applied between them, see Figure 2.

ANT provides:

• Spin-resolved coherent transmission spectrum T(E) ® Conductance
• Charge and spin population
• Orbital eigenchannel analysis
• Average electronic potential on atoms
• Current (I)
• Zero-bias conductance
• Differential conductance dI/dV
• Landauer transmission function
• DOS and projected DOS
• Population analysis
• Charge and Fermi level
• Calculation of hybridization functions to calculate electronic self-energy of strongly interacting electrons with impurity solvers
• Correlated charge and density matrix

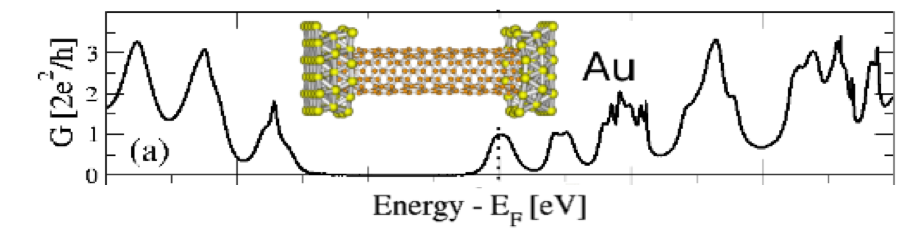
Figure 1. Example of transport calculation performed by ANT.G. The conductance of a six unit-cell (8,0) CNT contacted to Au is computed. Palacios J. J. et. al. Phys. Rev. B. 77, 113403 (2008)

ANT.G

Code designed as a generic computational tool with application in nanoelectronics. It provides an excellent compromise between computational cost and electronic structure definition as long as the aim is to compare with experiments where the precise atomic structure of the electrodes is not relevant or defined with precision.

Straightforward use of ANT.G includes the computation of the zero-bias conductance (or, alternatively, the electrical current under an applied bias voltage) of a variety of nanoscale systems such as molecular bridges or simply metallic atomic contacts as those created with scanning tunneling microscope or break junction techniques. The use of ANT.G may be naturally extended to the computation of scanning tunnelling spectroscopy and electrostatic force microscopy.

Makes use of the embedded cluster approach, which is associated with the use of the parametrized Tight-Binding (TB) Bethe Lattice (BL).

Embedded cluster approach

In such approach the scattering region is described with the Density Functional Theory (DFT) while the electrodes are described with a lower level of accuracy through the above mentioned BT lattice. This approach is valid because, while the detailed atomic and electronic structure of the device region is crucial, farther away from the scattering region these become less important. However, consequently, it is necessary to include a sufficiently wide section of the bulk electrodes in the device region so that the interface region between electrodes and scattering region is described properly. The model is generated by connecting a site with N nearest-neighbors in directions that can be those of a particular crystalline lattice.

The fact that this method cannot describe precisely the atomic structure of the electrodes can become useful when comparing the results with real experiments where the exact atomic geometry of the electrodes is not known and cannot be controlled in the experiment.

ANT.G is designed to have a low computational cost, thus, it becomes an excellent tool when dealing with big systems or if you wan to have “fast” prelimirary results.

The technical specifications are:

• Interface to the quantum chemistry GAUSSIAN03/09 code for practical implementation of the embedded cluster approach, associated with the use of parameterized tight-binding (TB) Bethe lattice model, see Figure 2.
• The electrodes are modelled by parameterized TB Bethe (BL) lattices. The model is generated by connecting a site with N nearest-neighbors in directions that can be those of a particular crystalline lattice.
• The advantage of choosing a BL over other models resides on the one hand in the lack of long-range order which mimics the polycrystallinity of real electrodes. On the other hand the BL captures the short-range order since the local coordination of an atom is that of an atom in the bulk crystal of the corresponding material.
• The electronic structure of the infinite system is calculated self-consistently only within a finite-size region (the scattering or device region containing the nanoconstriction or molecule) while the electronic structure of the rest of the system (i.e., the two bulk electrodes) is fixed from the very beginning to that of a simplified parameterized BL model.
• G is written in FORTRAN90 and uses OpenMP directives to take full advantage of multiprocessor nodes.
• It has been thoroughly tested with PGI compilers on various 32- and 64-bit platforms, see Figure 4.

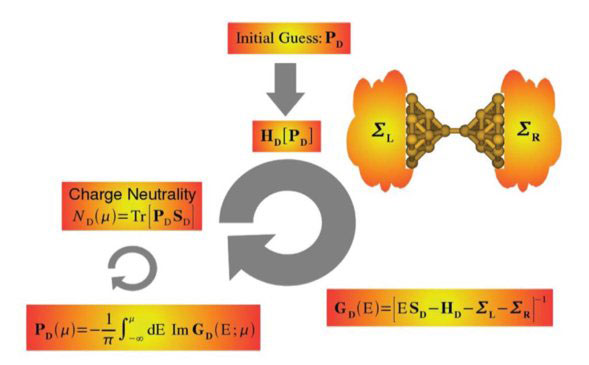
Figure 3.  Diagram illustrating the self-consistent procedure for calculating the electronic structure in the embedded cluster approach as implemented in ANT.G.  The central aspects of the used approach and of the one-body Green’s function and Landauer formalisms are given in D. Jacob and J. J. Palacios, J. Chem. Phys. 134,044118 (2011).

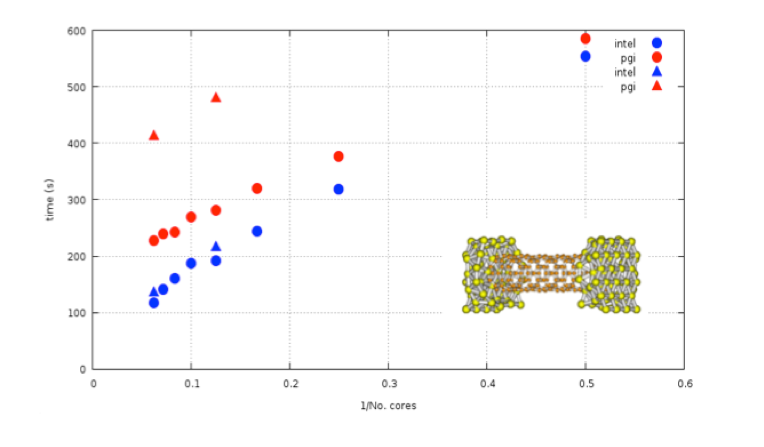
Figure 4. Performance of ANT.G in PGI and Intel compilers at low and high precision calculations

ANT.1D

Software specifically designed for the computation of the conductance at zero bias voltage in quasi-one-dimensional systems such as atomic chains, nanowires, carbon nanotubes, graphene nanoribbons, etc., which may present a disordered central region where scattering takes place. Other systems without an underlying one-dimensional symmetry such as molecular bridges can also be computed with ANT.1D by modeling the electrodes as finite-section quasi-one-dimensional wires.

ANT.1D is more demanding than ANT.G from the computational point of view, but presents the advantage of expanding the range of applicability of transport calculations to situations where the electrodes have a well-defined atomic structure.

ANT.1D has been tested with the gnu C++ compiler on various 32- and 64-bit platforms

Supercell approach

In this approach the electronic structure of the device region and the electrodes is calculated with ab-initio electronic structure codes for periodic systems that use localized basis sets such as CRSYTAL or SIESTA.

The system configuration of Left (L) anf Right (R) electrodes plus the central scattering or Device (D) region, see figure 5. In particular, the two leads L and R have to be connected where the electronic structure has relaxed to that of a bulk (i.e., infinite) nanowire thus, far enough away from the scattering region.

The technical specifications are:

• Practical implementation of the super-cell approach, where the electrodes are described by perfect nanowires, to calculate the electronic structure of the device and the leads, see Figure 5.
• In the super-cell approach, the model for the leads consists of semi-infinite nanowires with finite cross-section where the electronic structure is described at the same computational level as that of the device.
• 1D makes use of a pre-computed Hamiltonian for the scattering section and for the disorder-free regions. It can thus be used with tight-binding parameterized models or as a post-processing procedure to a one-dimensional periodic boundary conditions self-consistent electronic structure calculation using, e.g., CRYSTAL or SIESTA codes.
• 1D is completely written in FORTRAN90 and has been parallelized with MPI. It has been tested with the Intel compiler on various 32- and 64-bit platforms with and without MPI. It also been tested with the Portland group compiler, but only without MPI.It is written in Fortran 95 and memory is allocated dynamically. It may be compiled for serial or parallel execution (under MPI).
• The interface with the CRYSTAL03 and CRYSTAL06 code is written in ANSI C++, and has been tested with the gnu C++ compiler on various 32- and 64-bit platforms

Figure 4.  Illustration of the super-cell approach to calculate the electronic structure of the device and of the leads: (a) One-dimensional periodic system to calculate the electronic structure of the device region. (b) and (c): Infinite nanowires to calculate the electronic structure of the left (L) and right (R) semi-infinite leads. (d) Sketch of the setup of the physical system: The device region (D) is suspended between two semi-infinite leads L and R.  Further details of the method are given in D. Jacob and J. J. Palacios, J. Chem. Phys. 134,044118 (2011).

Basic functionalities of ANT.1D:

• Calculation of Landauer transmission function
• Calculation of DOS and projected DOS
• Population analysis
• Determination of Charge and Fermi level
• Interface with CRYSTAL06 ab-initio electronic structure code

Advanced functionality for treating strong electronic correlations:

• Calculation of hybridization functions to calculate electronic self-energy of strongly interacting electrons with impurity solvers
• Correlated transmission function
• Correlated DOS and PDOS
• Correlated charge and density matrix

ANT.U

This code is specifically designed for the computation of the conductance at zero bias voltage in, e.g., graphene-based systems using a one-orbital minimal model and on-site interactions (Hubbard model).

ANT.U is an easy-to-use program for the study of spin transport in 1D systems (fundamentally graphene-based systems like nanoribbons and nanotubes) which applies the Landauer formalism to tight-binding Hamiltonians with a local Coulomb interaction (U).

The local Coulomb potential is obtained self-consistently using the mean-field Hubbard model.